드론제작
★모터 속도 제어
-컴퓨터에서 쿼드콥터로 속도 명령을 주어 모터의 속도를 제어.
★복합동작 제어
-컴퓨터에서 쿼드콥터로 복합 명령을 주어 동시에 4개의 모터를 각각의 속도로 차례로 회전시킨 다양한 움직임을 가능하게 한다
★이착륙 제어
-컴퓨터에서 비행체로 일정 높이 이착륙 명령을 주어 비행체가 일정높이까지 수직으로 이륙시킨 후 착륙시킨다.
-컴퓨터에서 비행체로 추락방지 명령을 주어 추락하는 비행체를 안전하게 착륙시킨다.
☆가속도 및 자이로 센서
1. 가속도 센서
가속도 센서는 Accelerometer 로 말 그대로 가속도를 측정하는 센서입니다. 가속도 센서가 3축이라 함은 센서가 3차원에서 움직일 때 x축, y축, z축 방향의 가속도를 측정할 수 있다는 의미입니다. 기본적으로 가속도 센서는 가만히 정지한 상태에서 중력 가속도를 감지하기 때문에 z축 방향으로 -g 만큼의 값을 출력합니다. 그러면 이러한 가속도 센서를 이용해서 어떻게 자세, 즉 기울어진 각도를 측정할 수 있을까요?
먼저 움직이는 물체와 견고하게 센서가 장착되어 있는 상태에서 시작합니다. 센서의 초기 출력은 모두 0이라고 합시다. 이 상태에서 물체를 y축 방향으로 45도 기울여 보면, 기울어진 상태에서 z축 방향과 x축 방향으로 동일한 값의 가속도가 측정됩니다. 아래 그림 보시면 쉽게 이해가 되실텐데 중력방향으로 g 가 측정되어야 하므로 0.707g 만큼 z축과 x축 방향으로 값이 출력됩니다. 결과적으로는 z축과 x축 값의 비율을 atan 에 넣으면 그 결과값이 45도, 즉 기울어진 값을 알수 있습니다.
간단히 가속도 센서를 이용해서 각도를 측정하는 방법은 위와 같습니다. 하지만 간단한 만큼 문제점이 있습니다. 정지된 상태에서 물체가 움직이기 시작하면 그때 측정되는 값은 기울기를 나타내지 않을 수 있습니다. 예를 들어 45도 기울어진 위와 같은 상태에서 오른쪽으로 가속을 해본다고 가정해 보죠. 그러면 x축과 z축에서 측정되는 가속도는 변하게 됩니다. 한쪽값이 더 커지겠죠? 그러면 이 상태에서 atan 에 대입한다고 하더라도 45도 값은 나오지 않게 됩니다. 즉 움직임이 생겨서 어느 한쪽 방향으로 가속도가 생기게 되면 결과적으로 이 값이 중력에 의해 측정되는 가속도값과 구분이 안되게 됩니다.
* 정지하지 않은 움직임 상태에서는 가속도 센서만으로 기울기 값을 측정할 수가 없습니다.
2. 자이로 센서

자이로 센서는 가속도를 측정하는 가속도 센서와 달리 각속도를 측정합니다. 자이로스코프가 각속도를 측정하는 기구인데 MEMS 기술을 적용한 칩형태의 자이로센서도 각속도를 측정하는 기능을 가지는 것입니다. 각속도는 시간당 회전하는 각도를 의미하죠? 다음과 같은 예를 들어서 자이로 센서값이 어떻게 측정되는지 알아보겠습니다.
1. 수평한 자세를 유지하고 있는 상태를 가정합시다. 이때는 정지 상태이니 당연히 각속도도 0도/sec를 나타낼 것입니다.
2. 이 물체가 10초 동안 50도만큼 기울어진다고 봅시다. 이 10초동안은 0이 아닌 각속도 값을 가지게 됩니다. 10초 동안의 평균 각속도는 5도/sec 가 될것입니다.
3. 기울어지는 동작을 한 후 다시 멈춰서 50도를 유지한다고 봅시다. 이때는 다시 각속도가 0도/sec 가 됩니다.
1번 2번 3번 과정을 거치면서 각속도는 0 -> 5 -> 0으로 바뀌었습니다. 그런데 각도는 어떻게 바뀌었나요? 0도에서 점차 증가해서 50도가 되었습니다. 각속도에서 각도를 구하려면 전체 시간에 해당하는 만큼 적분을 해야합니다. 자이로 센서는 이와 같이 각속도를 출력으로 내보내기 때문에 전체 시간동안 이 각속도를 적분하면 기울어진 각도를 계산할 수 있습니다. 그런데 자이로 센서에도 문제점은 존재합니다. 적분의 문제점이지요. 센서에서 측정되는 각속도는 노이즈가 생기든 어떠한 이유에 의해 측정값에 에러가 계속 생기는데, 이 오차가 적분시에는 누적이 되어서 최종 값이 드리프트 되는 현상이 생깁니다.
* 자이로 센서에서 측정되는 각속도를 이용하면 시간이 지날수록 각도는 오차가 생겨 기울기 값이 변하게 됩니다.
가속도 센서와 자이로 센서를 이용해서 물체가 기울어진 각도를 측정하는 방법에 각각의 문제점이 존재하는데 정리하면 다음과 같습니다.
정지한 물체가 움직이기 시작한 후 다시 정지하는 동작을 한다면...
정지상태의 긴 시간의 관점에서 보면 가속도 센서에 의해 계산된 기울어진 각도는 올바른 값을 보여줍니다. 그러나 자이로 센서에서는 시간이 지날 수록 틀린 값을 나타냅니다.
반대로, 움직이는 짧은 시간의 관점에서 보자면 자이로 센서는 올바른 값을 보여줍니다. 하지만 가속도 센서는 기울어진 각도와는 영 다른 계산값이 나올겁니다.
결론적으로는 가속도센서와 자이로센서를 모두 사용해서 각각의 단점을 보상할 수 있는 알고리즘을 적용해서 롤 또는 피치 값을 계산하게 되는 것입니다. 많이 적용하는 보상 방법 및 필터링으로는 칼만필터를 사용하는 경우가 많이 있는데, 이 부분까지 알려면 공부를 많이 해야겠습니다.
Yaw 값 측정 Yaw 의 회전축은 z축방향, 즉 중력방향과 같습니다. 따라서 가속도센서보다는 자이로 센서의 z축 값을 측정해서 이 값을 이용해 yaw 값을 계산하고 드리프트되는 오차를 보상하는 다른 센서를 추가적으로 사용합니다. 바로 마그네토미터, 즉 지자기센서입니다. 3축 지자기 센서를 적용해서 yaw 방향을 측정하는 것입니다.
자이로는 온도가 변하면 그 값이 같이 변하는 특성이 있다고 합니다. 그래서 정확한 출력을 계산해야 할 경우 온도센서도 함께 사용해서 오차를 보상해야 합니다. 그래서 각도측정 센서를 찾아보면 보통 가속도센서, 자이로센서, 지자기센서, 온도센서를 내장한 9축 자세 측정 센서라고 합니다.
칼만 필터(Kalman filter)
칼만 필터(Kalman filter)는 잡음이 포함되어 있는 선형 역학계의 상태를 추적하는 재귀 필터로, 루돌프 칼만이 개발하였다. 칼만 필터는 컴퓨터 비전, 로봇 공학, 레이더 등의 여러 분야에 사용되며, 많은 경우에 매우 효율적인 성능을 보여준다.
이 알고리즘은 시간에 따라 진행한 측정을 기반으로 한다. 해당 순간에만 측정한 결과만 사용한 것보다는 좀 더 정확한 결과를 기대할 수 있다. 잡음까지 포함된 입력 데이터를 재귀적으로 처리하는 이 필터로서, 현재 상태에 대한 최적의 통계적 예측을 진행할 수 있다.
알고리즘 전체는 예측과 업데이트의 두 가지로 나눌 수 있다. 예측은 현재 상태의 예측을 말하며, 업데이트는 현재 상태에서 관측된 측정까지 포함한 값을 통해서 더 정확한 예측을 할 수 있는 것을 말한다.
확장 칼만 필터는 비선형 시스템을 기반으로 동작한다.
칼만 필터는 물체의 측정값에 확률적인 오차가 포함되고, 또한 물체의 특정 시점에서의 상태는 이전 시점의 상태와 선형적인 관계를 가지고 있는 경우 적용이 가능하다. 예를 들어, 레이더 추적의 경우 특정 물체의 위치, 속도, 가속도 등을 측정할 수 있지만 이 측정값에 오차가 포함되어 있을 수 있다. 이 경우, 연속적으로 측정하는 값들을 칼만 필터를 이용해서 해당 물체의 위치를 추정할 수 있다.
특정 시간  에서의 상태 벡터를
에서의 상태 벡터를 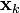 라고 정의하고, 또한 그 시간에서의 사용자 입력을
라고 정의하고, 또한 그 시간에서의 사용자 입력을  라고 정의할 때, 칼만 필터에서는 다음과 같은 관계식을 가정하고 있다.
라고 정의할 때, 칼만 필터에서는 다음과 같은 관계식을 가정하고 있다.
 에서의 상태 벡터를
에서의 상태 벡터를 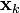 라고 정의하고, 또한 그 시간에서의 사용자 입력을
라고 정의하고, 또한 그 시간에서의 사용자 입력을  라고 정의할 때, 칼만 필터에서는 다음과 같은 관계식을 가정하고 있다.
라고 정의할 때, 칼만 필터에서는 다음과 같은 관계식을 가정하고 있다.
또한, 상태 벡터 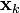 와 그 벡터를 측정했을 때 실제로 얻어진 벡터
와 그 벡터를 측정했을 때 실제로 얻어진 벡터  는 다음과 같은 관계식을 가지고 있다.
는 다음과 같은 관계식을 가지고 있다.
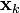 와 그 벡터를 측정했을 때 실제로 얻어진 벡터
와 그 벡터를 측정했을 때 실제로 얻어진 벡터  는 다음과 같은 관계식을 가지고 있다.
는 다음과 같은 관계식을 가지고 있다.
또한, 초기 상태와 각 잡음 변수 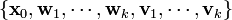 는 모두 상호 독립이라는 가정이 필요하다.
는 모두 상호 독립이라는 가정이 필요하다.
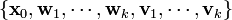 는 모두 상호 독립이라는 가정이 필요하다.
는 모두 상호 독립이라는 가정이 필요하다.
많은 경우, 실제 동적 시스템이 이 모델에 정확히 부합하지는 않는다. 특히, 선형성이나 상호 독립과 같은 중요한 가정이 맞지 않는 시스템의 경우, 칼만 필터의 성능을 심각하게 떨어뜨릴 수도 있고, 값을 발산하게 만드는 경우도 있다.
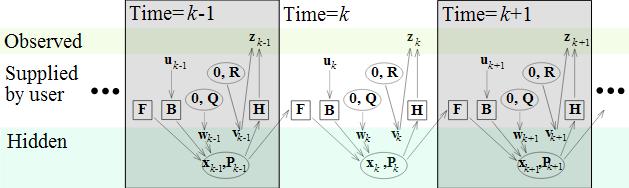
칼만 필터는 재귀적으로 동작한다. 즉, 칼만 필터는 바로 이전 시간에 추정한 값을 토대로 해서 현재의 값을 추정하며, 또한 바로 이전 시간 외의 측정값이나 추정값은 사용되지 않는다.
각 추정 계산은 두 단계로 이루어지며, 먼저 이전 시간에 추정된 상태에 대해, 그 상태에서 사용자 입력을 가했을 때 예상되는 상태를 계산한다. 이 단계는 예측(prediction) 단계라고 부른다. 그 다음, 앞서 계산된 예측 상태와 실제로 측정된 상태를 토대로 정확한 상태를 계산한다. 이 단계는 보정(update) 단계라고 부른다.
각 시간의 추정 상태는 평균과 분산의 두 개의 변수로 표현된다. 정확하게는,
 : k 시점의 측정값을 토대로 한 k 시점의 상태 추정값
: k 시점의 측정값을 토대로 한 k 시점의 상태 추정값 : k 시점의 측정값을 토대로 한 k 시점의 상태 공분산행렬
: k 시점의 측정값을 토대로 한 k 시점의 상태 공분산행렬
여기에서 아랫첨자로 쓰인 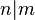 은 m 시점에서의 측정값을 토대로 한 n 시점의 상태 추정을 의미한다.
은 m 시점에서의 측정값을 토대로 한 n 시점의 상태 추정을 의미한다.
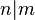 은 m 시점에서의 측정값을 토대로 한 n 시점의 상태 추정을 의미한다.
은 m 시점에서의 측정값을 토대로 한 n 시점의 상태 추정을 의미한다.예측 단계
예측 단계의 계산은 무지막지하게 이루어진다.
- 연역적 상태 예측:
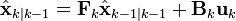
- 연역적 공분산 예측:

보정 단계
보정 단계에서는 앞단계의 예측 값과 실제 측정값간의 오차를 이용해, 이전에 얻은 값을 귀납적으로 수정한다.
- 예측 단계와 실제 측정간의 오차:
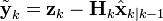
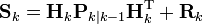
- 최적 칼만 이득(Kalman gain):
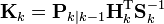
- 귀납적 상태 보정:

- 귀납적 공분산 보정:
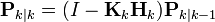
불변량
모델이 정확하고, 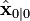 와
와 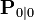 의 값이 정확하게 초기 상태 값의 몫을 반영한다면, 다음 불변량은 보존된다.
의 값이 정확하게 초기 상태 값의 몫을 반영한다면, 다음 불변량은 보존된다.
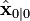 와
와 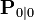 의 값이 정확하게 초기 상태 값의 몫을 반영한다면, 다음 불변량은 보존된다.
의 값이 정확하게 초기 상태 값의 몫을 반영한다면, 다음 불변량은 보존된다.
여기서 ![\textrm{E}[\xi]](https://upload.wikimedia.org/math/6/2/2/622bdf3feac7f49bbef4950f48b8fd45.png) 은
은  의 기대값이고, 공분산 매트릭스는 정확하게 추정의 공분산을 반영한다.
의 기대값이고, 공분산 매트릭스는 정확하게 추정의 공분산을 반영한다.
![\textrm{E}[\xi]](https://upload.wikimedia.org/math/6/2/2/622bdf3feac7f49bbef4950f48b8fd45.png) 은
은  의 기대값이고, 공분산 매트릭스는 정확하게 추정의 공분산을 반영한다.
의 기대값이고, 공분산 매트릭스는 정확하게 추정의 공분산을 반영한다.
Yaw Roll Pitch 란
3D세계에 존재하는 3개 방향의 회전축을 가리킨다.
지자기센서
지구자기장을 측정하는 센서. 측정 단위는 마이크로 테슬라(uT)
가장 간단한 것은 지침으로서,지자기의 방향을 직접 알 수 있을 뿐 아니라, 진동주기로부터 크기를 알 수 있다.
자침 이외에도 보다 감도 높게, 보다 간편하게 지자기를 검출하기 위해서 많은 센서가 개발되고 있다.
회전 코일을 사용한 자기의, 강자성체의 자기포화 현상을 이용한 포화 철심 형 자력계, 양성자의 핵자기 공명을 이용한 양자 자력계, 루비듐이나 세슘 원자의 제만효과를 이용한 광펌핑 자력계, 초전도현상을 이용한 SQUID 등이 있어 장점을 살려 사용되고 있다.
순수하게 X축에만 자기장이 검출되기 때문에 X축의 세기가 0.4G가 나와야 하지만 실제로는 주변 자기장 영향으로 0.4+a가 나오게 된다. 이것을 보정 모션을 통해 X축의 +방향으로 자북을 가리킬 때, -방향으로 가리킬 때를 체크하는 것이다.
이상적상황과 실제ㅔ적 상황에서의 x축 세기
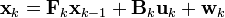
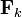 는 해당 시간에서 이전 상태에 기반한 상태 전이 행렬,
는 해당 시간에서 이전 상태에 기반한 상태 전이 행렬, 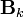 사용자 입력에 의한 상태 전이 행렬, 그리고
사용자 입력에 의한 상태 전이 행렬, 그리고  는
는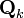 을 가지는
을 가지는  잡음 변수이다.
잡음 변수이다.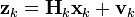
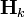 는 해당 시간에서 측정에 관계되는 행렬이고,
는 해당 시간에서 측정에 관계되는 행렬이고,  는
는  을 가지는
을 가지는  잡음 변수이다.
잡음 변수이다.![\textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k}] = \textrm{E}[\textbf{x}_k - \hat{\textbf{x}}_{k|k-1}] = 0](https://upload.wikimedia.org/math/c/9/2/c9203d41067d91d378d6856103fedfd2.png)
![\textrm{E}[\tilde{\textbf{y}}_k] = 0](https://upload.wikimedia.org/math/b/5/a/b5a54dc85106b58adbb9909c0b3fb1a3.png)
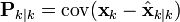
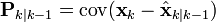

댓글 없음:
댓글 쓰기